Binomial adalah suatu ekspresi nilai yang diperoleh dari penjumlahan atau pengurangan dua suku. Atau binomial adalah polynomial dua suku. Menurut teorema ini, adalah mungkin untuk mengembangkan deret binomial (x + y)n menjadi jumlah yang melibatkan suku-suku dengan bentuk axmyn-m, di mana faktor pengali pada tiap suku ialah integer positif, dalam hal ini sembarang bilangan a. Faktor a disebut koefisien pada suku axmyn-m. Jumlah eksponen x dan y dalam tiap suku harus sama dengan n. Untuk memahami ini, walau agak aneh, perhatikan pola esponen m dan m-n pada suku axmyn-m dengan
Wednesday, November 6, 2013
TEOREMA BINOMIAL
Kata binomial berasal dari dua kata, yakni bi = dua, dan nomial = unsur atau variabel. Anda tak usah bingung jika kemudian menemukan istilah matematika Trinomial hingga Polynomial. Dalam aljabar permulaan, Teorema Binomial menjelaskan pengembangan aljabar pada suatu deret pangkat binomial.
Binomial adalah suatu ekspresi nilai yang diperoleh dari penjumlahan atau pengurangan dua suku. Atau binomial adalah polynomial dua suku. Menurut teorema ini, adalah mungkin untuk mengembangkan deret binomial (x + y)n menjadi jumlah yang melibatkan suku-suku dengan bentuk axmyn-m, di mana faktor pengali pada tiap suku ialah integer positif, dalam hal ini sembarang bilangan a. Faktor a disebut koefisien pada suku axmyn-m. Jumlah eksponen x dan y dalam tiap suku harus sama dengan n. Untuk memahami ini, walau agak aneh, perhatikan pola esponen m dan m-n pada suku axmyn-m dengan=n "n+(n-m)=n")
Contoh:
^3=x^{3}+3x^{2}y+3xy^{2}+y^{3} "(x+y)^3=x^{3}+3x^{2}y+3xy^{2}+y^{3}")
Faktor pengali yang muncul dalam pengembangan binomial disebut koefisien binomial. Koefisien binomial sama dengan entri segi tiga Pascal, dan boleh ditentukan melalui satu rumus mudah yang melibatkan faktorial. Angka-angka ini juga muncul dalam kombinatorik (matematika diskrit), di mana pekali xkyn−k sama dengan berbagai gabungan berlainan unsur-unsur k yang dapat dipilih daripada suatu sekumpulan n-unsur.
Menurut teorema ini, sebarang kuasa x+y dapat dikembangkan menjadi
^n=\binom{n}{0}x^n+\binom{n}{1}x^{n-1}y+\binom{n}{2}x^{n-2}y^2+\binom{n}{3}x^{n-3}y^3+...+\binom{n}{n-2}x^2y^{n-2}+\binom{n}{n-1}xy^{n-1}+y^n "(x+y)^n=\binom{n}{0}x^n+\binom{n}{1}x^{n-1}y+\binom{n}{2}x^{n-2}y^2+\binom{n}{3}x^{n-3}y^3+...+\binom{n}{n-2}x^2y^{n-2}+\binom{n}{n-1}xy^{n-1}+y^n")
Jika ditulis menggunakan simbol/notasi sigma, maka rumus perluasan binomial di atas menjadi
^n=\sum_{k=0}^{n}\binom{n}{k}x^{n-k}y{k} "(x+y)^n=\sum_{k=0}^{n}\binom{n}{k}x^{n-k}y{k}")
di mana 
ialah kombinasi k unsur diambil dari n unsur. dipakai untuk memeroleh koefisien binomial yang bersesuaian.Dengan nilai kombinasi
!)} "\binom{n}{k}=\frac{n!}{k!(n-k)!)}")
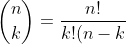Rumus ini kadang-kadang disebut rumus binomial atau rumus identitas binomial.
Supaya mudah, koefisien binomial dapat diambil dari segitiga Pascal berikut:
Perhatikan contoh-contoh berikut
Deret pangkat untuk mengikuti baris-baris segi tiga Pascal sbb:
Perhatikan baris terakhir segitiga Pascal, diperoleh:
Untuk jabaran dapat dibuat dengan memperhatikan tanda pada variabel y (bilangan negatif). Untuk Setiap bilangan negatif berlaku:
• jika pangkatnya genap hasilnya positif.
• Jika pangkatnya ganjil, hasilnya negatif.
Contoh
Binomial adalah suatu ekspresi nilai yang diperoleh dari penjumlahan atau pengurangan dua suku. Atau binomial adalah polynomial dua suku. Menurut teorema ini, adalah mungkin untuk mengembangkan deret binomial (x + y)n menjadi jumlah yang melibatkan suku-suku dengan bentuk axmyn-m, di mana faktor pengali pada tiap suku ialah integer positif, dalam hal ini sembarang bilangan a. Faktor a disebut koefisien pada suku axmyn-m. Jumlah eksponen x dan y dalam tiap suku harus sama dengan n. Untuk memahami ini, walau agak aneh, perhatikan pola esponen m dan m-n pada suku axmyn-m dengan
Subscribe to:
Post Comments (Atom)
Izin ya admin..:)
ReplyDeleteYuk dapatkan hadiah ny dengan modal 20rb saja sudah bisa menikmati semua permainan poker di ARENADOMINO loh yuk langsung saja.. WA +855 96 4967353
and after, since workers tend to schedule time off around them, leaving employees who opted not to take those days off with heavier workloads, thus reducing their productivity.
ReplyDelete수원출장샵
오산애인대행
김포애인대행
강진출장샵
애인대행